Dzhanibekov 효과

오늘날 탐구자를위한 물리학 분야의 무언가 : Dzhanibekov 효과테니스 라켓 정리라고도하는는 세 가지 관성 모멘트를 가진 회 전체의 불안정성을 설명합니다. 관성 모멘트는 회전 운동의 변화에 ​​대한 신체의 저항을 나타냅니다. 특정 회전 축과 형상에 따라 다릅니다. 고전적인 해밀턴 시스템의 역학을 이해하는 것은 수학적 설명을 훨씬 뛰어 넘는 수많은 응용 프로그램에서 여전히 중요한 목표입니다. 자유도가 거의없는 통합 시스템의 경우 효율적인 접근 방식은 기하학적 분석을 기반으로 기계 시스템의 동적 특성을 특성화합니다. 이러한 기하학적 현상은 일반적으로 실험적으로 관찰 할 수있는 특정 효과의 견고성의 기원입니다. 그들 중 하나는 소위 Dzhanibekov 효과 테니스 라켓 효과라고도합니다.

ISS의 무중력 상태에서 Dschanibekow 효과

이 현상의 우수하고 상세한 이론적 파생은 여기에서 찾을 수 있습니다 (https://arxiv.org/pdf/1606.08237.pdf). 우리는 여기서 조금 더 거칠지 만 그럼에도 불구하고 현상을 설명하는 사람을 다루고 있습니다. 불행히도 강체의 역학에 대한 사전 지식이 필요합니다.

I1이 가장 작고 I2이 가장 큰 관성 모멘트 I3 및 I1 및 I3이있는 관성 행렬 (대각선)을 고려하십시오. 이제 주 관성 모멘트 I3의 축 주위의 움직임을 고려하십시오. 각속도 벡터는 다음과 같습니다.

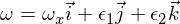
엡실론은 다른 두 개의 주요 축에서 작은 섭동입니다. 이제 이것을 오일러 방정식에 삽입하면 다음을 얻을 수 있습니다.

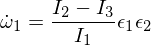
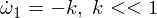
이제 두 번째 오일러 방정식을 미분합니다.

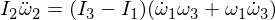
우리의 표현에서 오메가 1과 오메가 3를 대체하고 엡실론을 곱하면 무시할 수있을만큼 작아지기 때문에

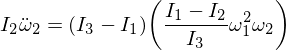
이것은 다음과 같은 형태의 오메가 2에 대한 미분 방정식을 제공합니다.

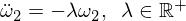
기본 솔루션은 다음과 같습니다.

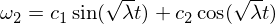
따라서 우리는 오메가 -1 축의 회전 장애가 안정적이고주기적인 운동을하거나 강체 운동이라는 용어로 세차 운동을한다는 ​​것을 알고 있습니다. 오메가 3 장애는 위와 유사한 주장을 따르며, 여러분이 그것을 극복 할 수 있도록 연습으로 남겨 두겠습니다. 중간 축의 경우 다음이 있습니다.

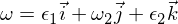
오일러 방정식에 삽입 :

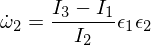
세 번째 오일러 방정식을 미분하면 다음이 제공됩니다.

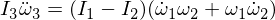
파생 된 표현식을 대체 해 보겠습니다.

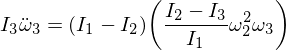
이제 다음 미분 방정식을 재정렬하고 유도하십시오.

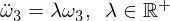
계수가 이제 양수이므로 지수 솔루션으로 이어집니다.

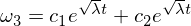
이 솔루션은 오메가 3이 오메가 2의 교란으로 중간 축을 따라 불안정하다는 것을 보여줍니다!

이것은 무엇을 의미합니까?

이제 우리는 정리를 이해하기 위해 우리가 도출하고 배운 모든 것을 결합 할 수 있습니다. 간단히 말해, 중간 축을 따라 회전이 방해를 받으면 지수 솔루션이있는 미분 방정식이 생성됩니다. 이것은 다른 두 축에서 관찰되는 정확한 움직임과 달리 불안정한 움직임으로 이어집니다. 이 결과는 매우 놀랍습니다. 중간 관성 모멘트가 왜 불안정한 회전을 초래하는지 상상할 수 없기 때문에 그러한 정리에 대한 직관적 인 지원이 없습니다. 본질적으로 순전히 수학적 인 것처럼 보입니다.